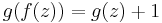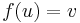Abel function
In mathematics Abel function is a special kind of solution of the Abel equations, used to classify them as superfunctions, and formulate conditions of uniqueness.
The Abel equation is class of equations which can be written in the form
where function ƒ is supposed to be given, and function g is expected to be found. This equation is closely related to the iterative equation
which is also called "Abel equation".
In general the Abel equation may have many solutions, and the additional requirements are necessary to select the only one among them.
Contents |
Superfunctions and Abel functions
Definition 1: Superfunction
If
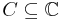 ,
, 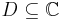
 is holomorphic function on
is holomorphic function on  ,
,  is holomorphic function on
is holomorphic function on 
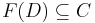
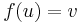
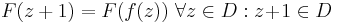
Then and only then
 is
is 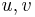 superfunction of
superfunction of  on
on 
Definition 2: Abel function
If
 is
is 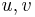 superfunction on
superfunction on  on
on 
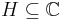 ,
, 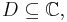
 is holomorphic on
is holomorphic on 
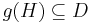
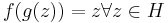
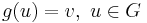
Then and only then
 id
id  Abel function in
Abel function in  with respect to
with respect to  on
on  .
.
References
- This article incorporates material from the Citizendium article "Abel function", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.